Starknet state
Starknet’s state consists of:
| Contract classes |
a mapping between the class hash and the class definition |
| Contract instances |
a mapping between addresses (251-bit field elements) and the contract’s state |
A contract instance’s state consists of:
| Class hash |
defines the functionality of the contract |
| Contract storage |
a key-value mapping where the key/values are field elements |
| Contract nonce |
the number of transactions sent from this contract |
Transitioning to a new state
A transaction \(tx\) transitions the system from state \(S\) to state \(S'\) if:
-
\(tx\) is an Invoke transaction, and the storage of \(S'\) is the result of executing the target contract code with respect to the previous state \(S\). The arguments, contract instance’s address, and the specific function entry point are part of the transaction.
-
\(tx\) is a Deploy account transaction, and \(S'\) contains the new contract instance’s state at the contract instance’s address. Additionally, the storage of \(S\) is updated according to the execution of the contract instance’s constructor.
-
\(tx\) is a Declare transaction, and \(S'\) contains the class hash and definition in the contract class’s mapping
State commitment
The state commitment is a digest that represents the state.
In Starknet, the state commitment combines the roots of two binary Merkle-Patricia tries of height 251 in the following manner:
state_commitment = hPos(
"STARKNET_STATE_V0",
contract_trie_root,
class_trie_root
)
Where:
-
hPosis the Poseidon hash function. -
STARKNET_STATE_V0is a constant prefix string encoded in ASCII (and represented as a field element). -
contract_trie_rootis the root of the contract trie, a Merkle-Patricia trie whose leaves are the contracts' states. -
class_trie_rootis the root of the class trie, a Merkle-Patricia trie whose leaves are the compiled class hashes.
The contract trie
As with Ethereum, this trie is a two-level structure, whose leaves correspond to distinct contracts. The address of each contract determines the path from the trie’s root to its corresponding leaf, whose content encodes the contract’s state.
The information stored in the leaf is as follows:
hPed(
hPed(
hPed(
class_hash,
storage_root
),
nonce
),
0
)
Where:
-
hPedis the Pedersen hash function. -
class_hashis the hash of the contract’s definition. -
storage_rootis the root of another Merkle-Patricia trie of height 251 that is constructed from the contract’s storage. -
nonceis the current nonce of the contract.
The class trie
The class trie encodes the information about all existing classes in Starknet’s state. This trie maps class hashes to their compiled class hashes. The information stored in a leaf at a path corresponding to some class hash is as follows:
hPos(
CONTRACT_CLASS_LEAF_V0,
compiled_class_hash
)Where:
-
hPosis the Poseidon hash function -
CONTRACT_CLASS_LEAF_V0is a constant prefix string encoded in ASCII (and represented as a field element). -
compiled_class_hashis the hash of the Cairo assembly resulting from compiling the given class via the Sierra-to-Casm compiler.
|
Compiled class hash
The compiled class hash identifies the output of a specific Casm compilation as unique. Cairo classes that are part of the state commitment are defined with Sierra, an intermediate representation between Cairo and Cairo assembly (Casm). However, the prover only works with Casm. So in order to prevent needing to compile from Sierra to Casm in every block in which the class is used, the state commitment must have some information about the corresponding Cairo assembly. The compiled class hash provides this information. For more information, see Cairo and Sierra. The party that declares the contract signs the compiled class hash, which they obtain using an SDK, as part of the In the future, when Sierra-to-Casm compilation becomes part of the Starknet OS, this value might be updated via a proof of the Sierra-to-Casm compiler execution, showing that compiling the same class with a newer compiler version results in some new compiled class hash. |
Merkle-Patricia trie
The state commitment scheme uses a binary Merkle-Patricia trie with the Pedersen hash function.
About nodes
Each node in the trie is represented by a triplet \((length, path, value)\), where:
| \(length\) |
is the length of the path, measured in nodes. |
| \(path\) |
is the path from the current node to its unique non-empty subtrie. \(path\) is an integer in the set \(\{0,\ldots,2^{length}-1\}\), and the binary expansion of \(path\) indicates how to proceed along the trie, as follows:
|
| \(value\) |
is the value of the node, which can be either data, or the hash of two non-empty child nodes. |
An empty node is one whose triplet values are \((0,0,0)\). Leaf nodes and internal nodes can be empty. A subtrie rooted at a node \((length, path, value)\) has a single non-empty subtrie, rooted at the node obtained by following the path specified by \(path\).
|
Length is specified, and cannot be deduced from \(path\), because the numbers in the triplet \((length, path, value)\) are field elements of fixed size, 251 bits each. For a node where \(length>0\), \(path\) leads to the highest node whose left and right children are not empty. |
Trie construction
The following rules specify how the trie is constructed from a given set of leaves:
The hash of a node \(N =(length, path, value)\), denoted by \(H(N)\), is:
|
All arithmetic operations in the above description of \(H\) are done in the STARK field, as described in The STARK field. |
Mathematical definition of the nodes in the trie
The triplet representing the parent of the nodes \(left=(\ell_L, p_L, v_L)\), \(right=(\ell_R, p_R, v_R)\) is defined as follows:
Example trie
The diagram A three-level Merkle-Patricia trie illustrates the construction of a three-level-high Merkle-Patricia trie from the leaves whose values are \((0,0,1,0,0,1,0,0)\):
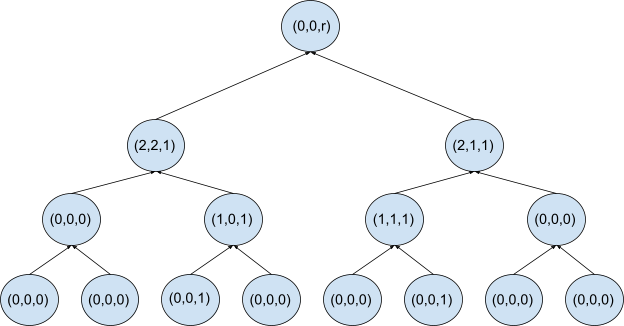
Where \(r=h_{Ped}(H(2,2,1),H((2,1,1))\). Notice that the example does not skip from the root, whose length is zero, so the final state commitment to the trie is \(H((0,0,r))=r\).
Suppose that you want to prove, with respect to the state commitment just computed, that the value of the leaf whose path is given by \(101\) is \(1\). In a standard Merkle trie, the proof would consist of data from three nodes, which are siblings along the path to the root.
In a Merkle-Patricia trie, because the trie is sparse, you only need to send the two children of the root, which are \((2,2,1)\) and \((2,1,1)\). These two children are enough to reproduce the state commitment \(r\), and because you know that the height of the trie is three, and that it is fixed, you know that the path \(01\) of length \(2\) specified by the right-hand child, \((2,1,1)\), leads to the desired leaf.
Special addresses
Starknet uses special contract addresses to provide distinct capabilities beyond regular contract deployment.
Two such addresses are 0x0 and 0x1. These addresses are reserved for specific purposes and are
characterized by their unique behavior in comparison to traditional contract addresses.
Address 0x0
Address 0x0 functions as the default caller_address for external calls, including interactions with the L1 handler or deprecated Deploy transactions. Unlike regular contracts, address 0x0 does not possess a storage structure and does not accommodate storage mapping.
Address 0x1
Address 0x1 is another special contract address within Starknet’s architecture. It functions as a storage space for mapping block numbers to their corresponding block hashes. The storage structure at this address is organized as follows:
| Keys |
Block numbers between \(\text{first_v0_12_0_block}\) and \(\text{current_block - 10}\). |
| Values |
Corresponding block hashes for the specified blocks. |
| Default Values |
For all other block numbers, the values are set to |
The storage organization of address 0x1 supports the efficient retrieval of block hashes based on block numbers within a defined range and is also used by the get_block_hash system call.