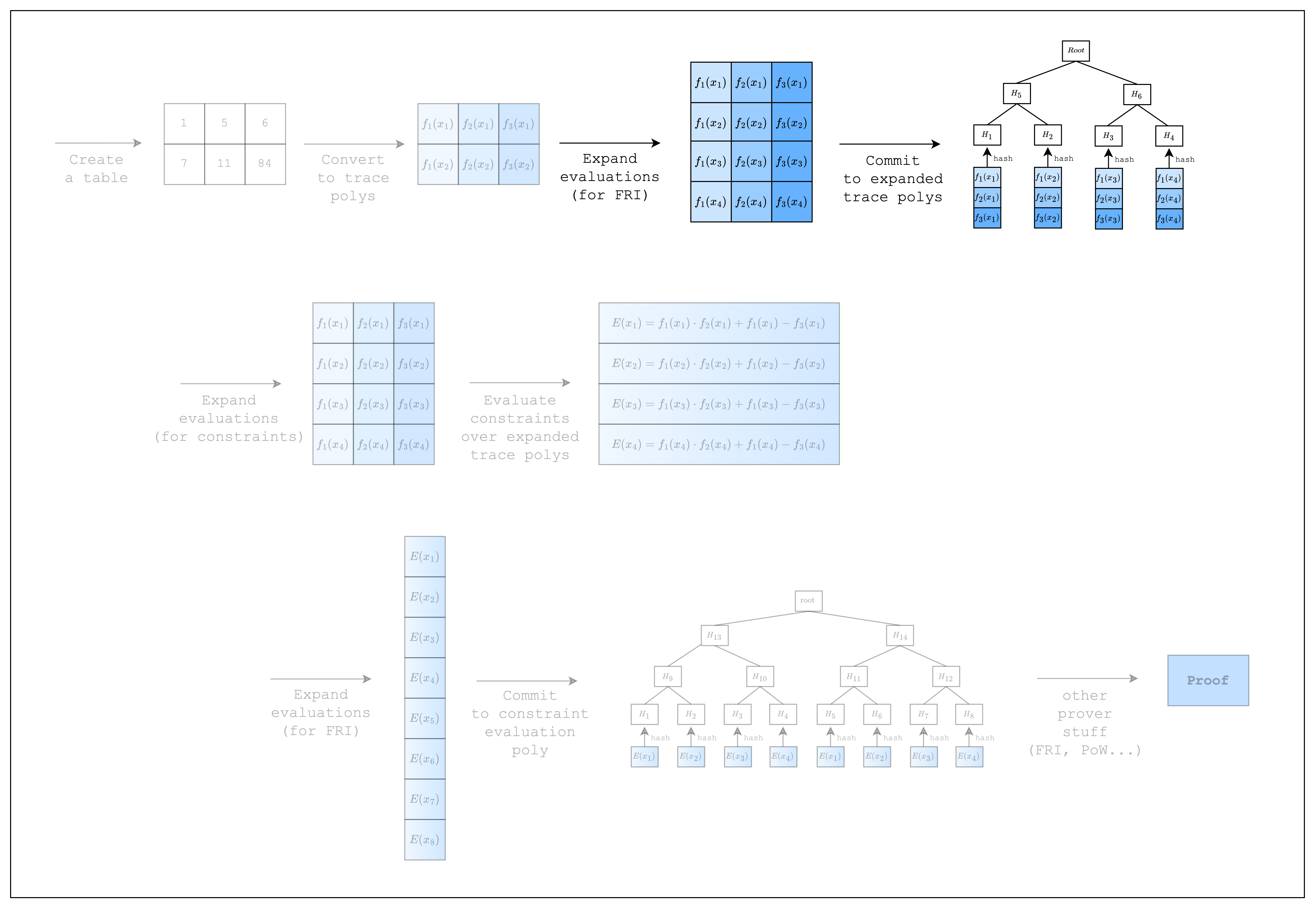
Figure 1: Prover workflow: Commitment

Now that we have created the trace polynomials, we need to commit to them. S-two commits to the trace polynomials by first expanding the trace polynomials (i.e. adding more evaluations) and then committing to the expanded evaluations using a merkle tree. The rate of expansion (commonly referred to as the blowup factor) is a parameter of FRI and readers who are interested in learning more about how to set this parameter can refer to the Circle-STARKs paper. (We are also working on adding an explanation in the book). For the puposes of this tutorial, we will use the default values for the blowup factor. 
use stwo_prover::core::{
    backend::{
        simd::{
            column::BaseColumn,
            m31::{LOG_N_LANES, N_LANES},
            SimdBackend,
        },
        Column,
    },
    channel::{Blake2sChannel, Channel},
    fields::m31::M31,
    pcs::{CommitmentSchemeProver, PcsConfig},
    poly::{
        circle::{CanonicCoset, CircleEvaluation, PolyOps},
        BitReversedOrder,
    },
    vcs::blake2_merkle::Blake2sMerkleChannel,
    ColumnVec,
};

const CONSTRAINT_EVAL_BLOWUP_FACTOR: u32 = 1;

fn main() {
    let num_rows = N_LANES;
    let log_num_rows = LOG_N_LANES;

    // Create the table
    let mut col_1 = BaseColumn::zeros(num_rows);
    col_1.set(0, M31::from(1));
    col_1.set(1, M31::from(7));

    let mut col_2 = BaseColumn::zeros(num_rows);
    col_2.set(0, M31::from(5));
    col_2.set(1, M31::from(11));

    // Convert table to trace polynomials
    let domain = CanonicCoset::new(log_num_rows).circle_domain();
    let trace: ColumnVec<CircleEvaluation<SimdBackend, M31, BitReversedOrder>> = vec![col_1, col_2]
        .into_iter()
        .map(|col| CircleEvaluation::new(domain, col))
        .collect();

    // Config for FRI and PoW
    let config = PcsConfig::default();

    // Precompute twiddles for evaluating and interpolating the trace
    let twiddles = SimdBackend::precompute_twiddles(
        CanonicCoset::new(
            log_num_rows + CONSTRAINT_EVAL_BLOWUP_FACTOR + config.fri_config.log_blowup_factor,
        )
        .circle_domain()
        .half_coset,
    );

    // Create the channel and commitment scheme
    let channel = &mut Blake2sChannel::default();
    let mut commitment_scheme =
        CommitmentSchemeProver::<SimdBackend, Blake2sMerkleChannel>::new(config, &twiddles);

    // Commit to the preprocessed trace
    let mut tree_builder = commitment_scheme.tree_builder();
    tree_builder.extend_evals(vec![]);
    tree_builder.commit(channel);

    // Commit to the size of the trace
    channel.mix_u64(log_num_rows as u64);

    // Commit to the original trace
    let mut tree_builder = commitment_scheme.tree_builder();
    tree_builder.extend_evals(trace);
    tree_builder.commit(channel);
}
We begin with some setup. First, we create a default PcsConfig instance, which sets the values for the FRI and PoW operations. Setting non-default values is related to the security of the proof, which is out of the scope for this tutorial. Next, we precompute twiddles, also known as the domain over which the rows in the table are evaluated on. The log size of this domain is set to log_num_rows + CONSTRAINT_EVAL_BLOWUP_FACTOR + config.fri_config.log_blowup_factor, which is the max log size of the domain that is needed throughout the proving process. Why we need to add CONSTRAINT_EVAL_BLOWUP_FACTOR will be explained in the next section. The final setup is creating a commitment scheme and a channel. The commitment scheme will be used to commit to the trace polynomials as merkle trees, while the channel will be used to keep a running hash of all data in the proving process (i.e. transcript of the proof). This is part of the Fiat-Shamir transformation where randomness can be generated safely even in a non-interactive setting. Here, we use the Blake2sChannel and Blake2sMerkleChannel for the channel and commitment scheme, respectively, but we can also use the Poseidon252Channel and Poseidon252MerkleChannel pair. Now that we have our setup, we can commit to the trace polynomials. But before we do so, we need to first commit to an empty vector called a preprocessed trace, which doesn’t do anything but is required by S-two. Then, we need to commit to the size of the trace, which is a vital part of the proof system that the prover should not be able to cheat on. Once we have done these, we can finally commit to the original trace polynomials.